Вчимося будувати графіки функцій за допомогою комп'ютера
Урок 3. Графік функції \(y=\sqrt{x}\)
Для того щоб відкрити програму GeoGebra, яка допомагатиме нам будувати графіки, перейдіть за посиланням https://www.geogebra.org/classic
Навчимося будувати графіки функцій \(y=\sqrt{x}\).
Для знака квадратного кореня в GeoGebra (як і в багатьох мовах програмування) використовується позначення sqrt(...) (скорочення від слів square root – квадратний корінь).
Для того щоб записати вираз \(\sqrt{x} \), у поле для вводу команд GeoGebra пишемо f(x)=sqrt(x).
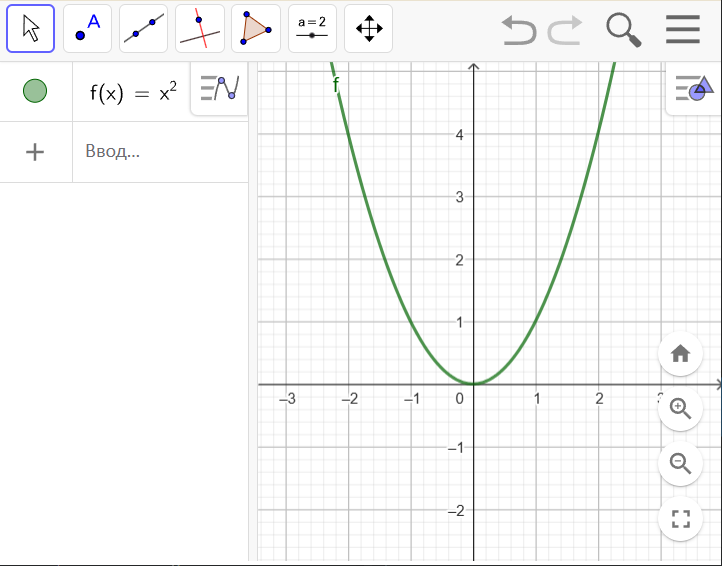Після цього з’явиться формула \(\sqrt{x} \), поле для вводу команд GeoGebra посунеться нижче, а на координатній площині з'явиться відповідний графік.
Наведемо ще декілька прикладів, як ввести формули, які містять квадратні корені:
| Формула | Вводимо |
|---|---|
| \(f(x) = \sqrt{x+0.2}\) | f(x) = sqrt(x+0.2) |
| \(f(x) = \sqrt{x}-4\) | f(x) = sqrt(x) - 4 |
| \(f(x) = \left(\frac{1}{\sqrt{x}}\right)^2 -1\) | f(x)=(1/sqrt(x)\(\to\))^2\(\to\)-1 |
Навчимося знаходити точки перетину графіків функцій \(f(x) =\frac{k}{x}\) і \(g(x)=\sqrt{x}\) залежно від значень параметра k.
Для цього нам потрібно створити засіб для зміни значення параметра k.
Виберіть команду "створити Повзунок" 
із панелі команд GeoGebra.
Далі клацніть мишею на координатній площині, бажано не в самому центрі. На цьому місці з'явиться повзунок після закінчення вводу його параметрів.
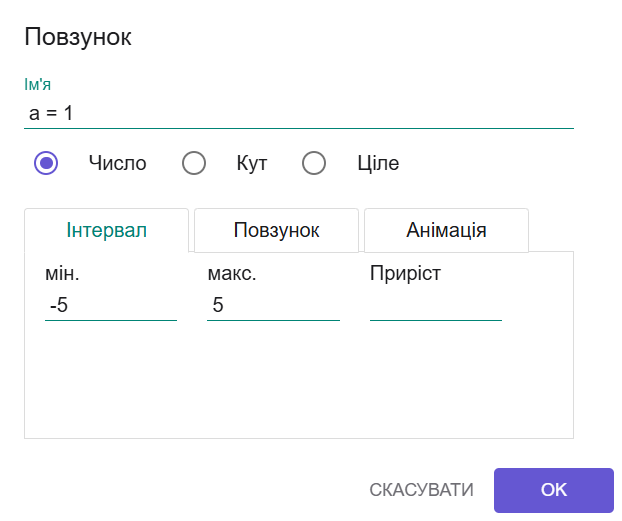Відкриється вікно для вводу параметрів повзунка.
У полі "Ім'я" ми можемо ввести ім'я параметра, тобто букву, якою позначено параметр та його початкове значення. Введемо k = 1.
Залишаємо вибір "Число". Інтервал зміни параметра можна поставити більшим від того, який ви зараз бачите на екрані, наприклад, від -10 до 10. Приріст, тобто крок, із яким буде змінюватися параметр, можна поставити, наприклад, 0.1.
Натискаємо кнопку OK.
Ми створили повзунок, який дозволяє змінювати значення параметра k. Потягнете повзунок праворуч – параметр збільшиться, потягнете ліворуч – зменшиться.
Не забудьте натиснути клавішу Esc або кнопку "Переміщення" 
, щоб скасувати активну команду "створити Повзунок".
Тепер задамо функцію, яка залежить від цього параметра. Будемо використовувати букву k у формулі, що задає функцію.
Введемо в поле вводу команд GeoGebra: f(x) = k / xEnter
Спробуємо потягати повзунок k в різні сторони. Бачимо, як змінюється графік залежно від значень параметра k.
Вище ми поставили завдання навчитися знаходити точки перетину графіків функцій \(f(x) =\frac{k}{x}\) і \(g(x)=\sqrt{x}\) залежно від значень параметра k
Задамо ще одну функцію. Вводимо: g(x) = sqrt(x)Enter. На координатній площині додасться графік функції \(g(x) = \sqrt{x}\).
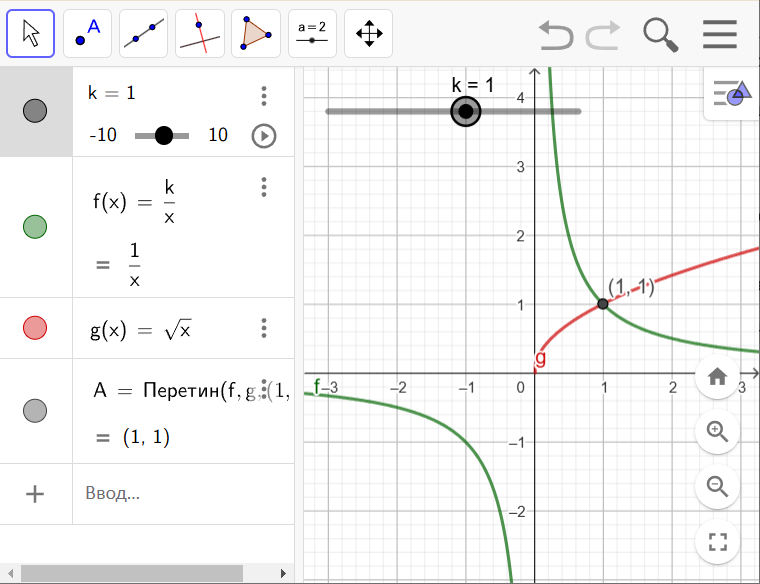Знову потягнемо повзунок k в різні сторони. Бачимо, як змінюються положення та кількість точок перетину графіків функцій f і g.
Можемо задати точки перетину функцій і вивести їхні координати на екран, як було описано в другому уроці.
Потренуйтеся вводити формули в GeoGebra:
| \(f(x) = 3\sqrt{x}\) |
| \(f(x) = \sqrt{\frac{x}{2}}\) |
| \(f(x) = \sqrt{\frac{1}{x}} - \sqrt{x}\) |
Потренуйтеся вводити формули з параметром і простежте, як змінюється графік залежно від значень параметра:
| \(f(x)=x^2-\frac{k}{x}\) |
| \(f(x)=x-\frac{k}{x-k}\) |
| \(f(x)=\frac{x^2}{k^4}-\frac{k}{x}\) |