Вчимося будувати графіки функцій за допомогою комп'ютера
Урок 2. Графік функції \(y=x^2\)
Для того щоб відкрити програму GeoGebra, яка допомагатиме нам будувати графіки, перейдіть за посиланням https://www.geogebra.org/classic
Навчимося будувати графіки функцій, де у формулі наявний степінь.
При вводі з клавіатури степінь відображається знаком ^. Наприклад, нам треба ввести формулу \(f(x)=x^2\).
У поле для вводу команд GeoGebra пишемо f(x)=x^2 Enter.
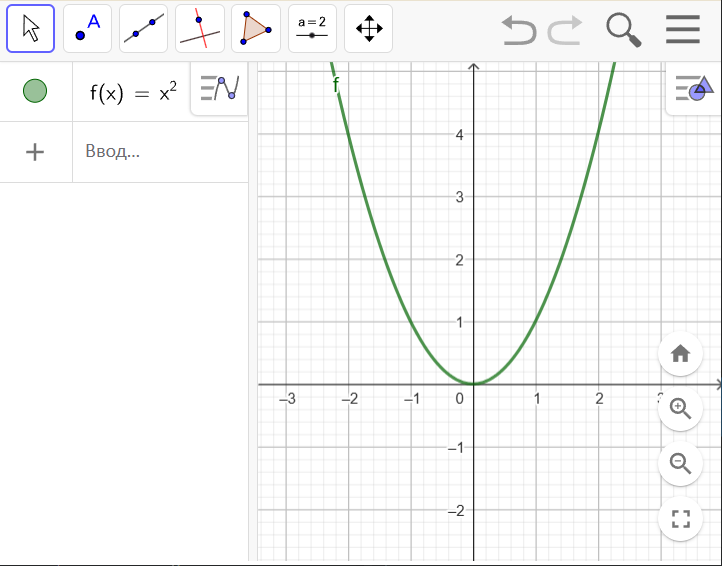Після цього з’явиться формула \(f(x)=x^2\), поле для вводу команд GeoGebra посунеться нижче, а на координатній площині з'явиться відповідний графік.
Коли ви вводите формулу зі степенем і хочете, щоб курсор покинув показник степеня, треба натиснути стрілочку вправо (\(\to\)).
Наприклад, вираз \(x^2+1\) вводимо так: x^2\(\to\)+1.
Спробуйте замінити вже побудований графік функції на графік функції \(f(x)=x^2+1\).
Наведемо ще декілька прикладів, як ввести формули, які містять степені :
| Формула | Вводимо |
|---|---|
| \(f(x)=0.5x^2-\frac{1}{3}\) | f(x)=0.5x^2\(\to\)-1/3\(\to\) |
| \(f(x)=(x-1)^2-0.91\) | f(x)=(x-1)^2\(\to\)-0.91 |
| \(f(x) = \frac{1}{12} \frac{(x-2)^2}{1-x} - 0.4\) | f(x) = 1/12\(\to\)((x-2)^2\(\to\))/(1-x)\(\to\) - 0.4 |
Навчимося знаходити координати точок перетину графіків функцій.
Розглянемо графіки функцій \(f(x)=x^2\) та \(g(x)=0.5(x+1)\).
Введемо в поле вводу команд GeoGebra
f(x)=x^2\(\to\)+1Enter
g(x)=0.5(x+1)
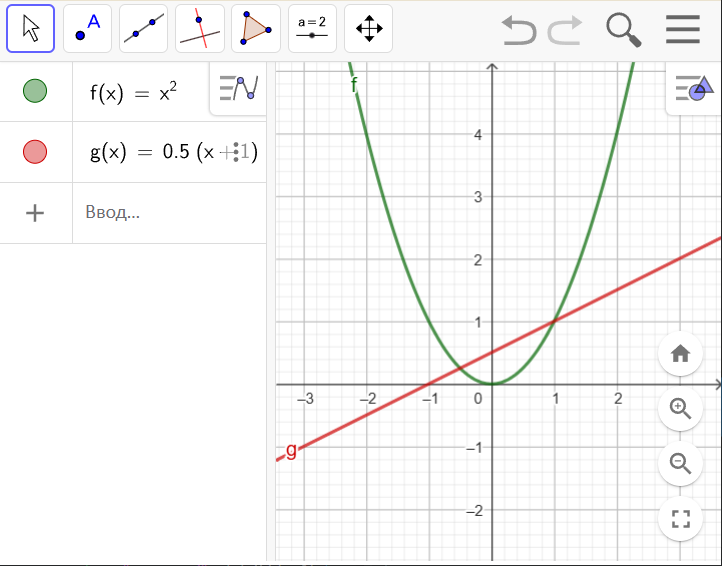Програма побудує графіки цих функцій.
Візуально ми бачимо точки їх перетину, але хотілося б, щоби програма відобразила їхні координати. Давайте навчимося це робити.
Виберемо мишею інструмент "Точка"
на верхній панелі GeoGebra. Коли інструмент вибрано, то його іконка на панелі підсвічена блакитною рамкою.
Перемістіть вказівник миші до місця перетину графіків функцій f і g та натисніть ліву кнопку миші. Намагайтеся натискати кнопку саме тоді, коли вказівник миші над точкою перетину.
Після цього поверніть поточний інструмент GeoGebra на кнопку "Переміщення" 
, як було спочатку. Для цього натисніть на кнопку "Переміщення" мишею або натисніть клавішу Esc.
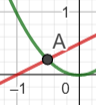Програма відобразила точку та її ім'я (точка А, точка В тощо), а ми хочемо бачити її координати. Відкриємо налаштування цієї точки (правою кнопкою миші клацаємо на точку, вибираємо 
). У закладці "Основні" знаходимо поле "Показати позначення". Вибираємо біля нього з випадного списку пункт "Значення".
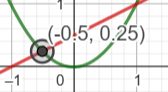Біля точки відображатимуться її координати.
Радимо вам перевірити: в закладці "Основні" в полі "Визначення" повинно бути написано
Перетин (g , f, (якісь координати або число)): 
Це означає, що ми поставили точку саме на перетині графіків функцій f і g, а не десь поруч.
Також у панелі "Налаштування" ми можемо змінити зовнішній вигляд цієї точки в закладках "Колір" та "Стиль".
Потренуйтеся вводити формули в GeoGebra:
| \(f(x) = x^2-2\) |
| \(f(x) = \frac{1}{13}x^2\) |
| \(f(x) = (x+1)^2-1\) |
| \(f(x) = \frac{1}{12}\frac{(x-2)^2}{1-x}-0.4 \) |
Знайдіть координати спільних точок графіків функцій:
| \(f(x) = 2x - 4\); | \(g(x) = \frac{6}{x}\) |
| \(f(x) = 3x + 4\); | \(g(x) = x^{2}\) |
| \(f(x) = - \frac{2}{x}\); | \(g(x) = x^{2} - 3 \) |