Вчимося будувати графіки функцій за допомогою комп'ютера
Урок 1. Графік функції \(y=\frac{k}{x}\)
Для того щоб відкрити програму GeoGebra, яка допомагатиме нам будувати графіки, перейдіть за посиланням https://www.geogebra.org/classic
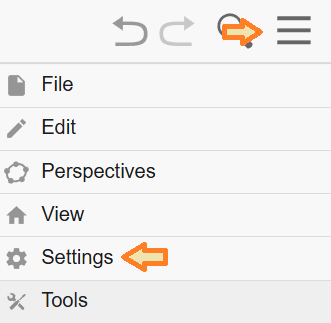 Якщо у вас програма відображається англійською мовою, то натисніть на кнопку меню, оберіть пункт "Settings", а далі виберіть українську мову.
Якщо у вас програма відображається англійською мовою, то натисніть на кнопку меню, оберіть пункт "Settings", а далі виберіть українську мову.
Для початку навчимося будувати графік лінійної функції.
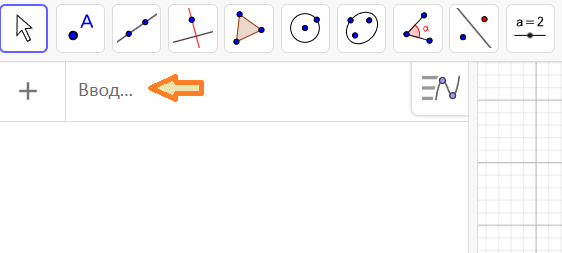 Клацніть мишею на поле для вводу команд GeoGebra у верхньому лівому куті і введіть за допомогою англійської розкладки на клавіатурі формулу, що задає функцію, графік якої ви хочете побудувати. Наприклад, f(x) = 2x-1
Клацніть мишею на поле для вводу команд GeoGebra у верхньому лівому куті і введіть за допомогою англійської розкладки на клавіатурі формулу, що задає функцію, графік якої ви хочете побудувати. Наприклад, f(x) = 2x-1
Після закінчення вводу натисніть клавішу Enter.
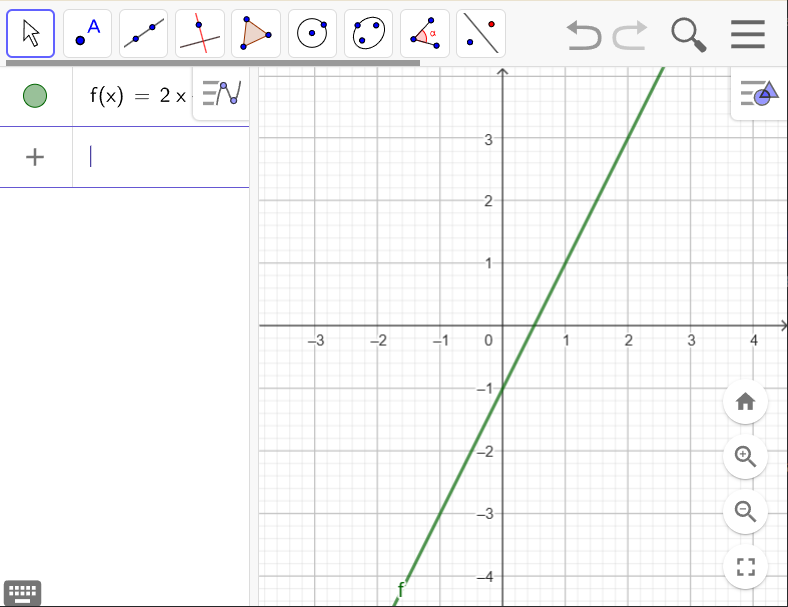 На координатній площині з’явився графік функції, яку ви задали формулою.
На координатній площині з’явився графік функції, яку ви задали формулою.
Ви можете змінити його колір і товщину лінії. Для цього підведіть курсор до графіка, а потім натисніть праву кнопку миші та виберіть пункт ![]() .
.
Відкриється панель налаштувань. У закладці "Колір" можна змінювати колір графіка. У закладці "Стиль" – товщину лінії та її прозорість.
Закрийте панель, натиснувши на хрестик справа![]() .
.
Тепер побудуємо інший графік.
Ми можемо видалити вже намальований графік лінійної функції або змінити формулу, яка задає іншу функцію.
Для того щоб видалити старий графік, клацніть на графік мишею та натисніть клавішу Delete (або виберіть дію ![]() ) з випадного меню.
) з випадного меню.
Для того щоб змінити формулу, клацніть на неї та внесіть необхідні виправлення.
Побудуємо графік функції \(f(x)=\frac{2}{x}\)
Для того щоб записати звичайний дріб, введіть спочатку чисельник, потім натисніть символ / та введіть знаменник. Тобто в полі для вводу команд GeoGebra пишемо: f(x)=2/x. Потім натискаємо Enter.
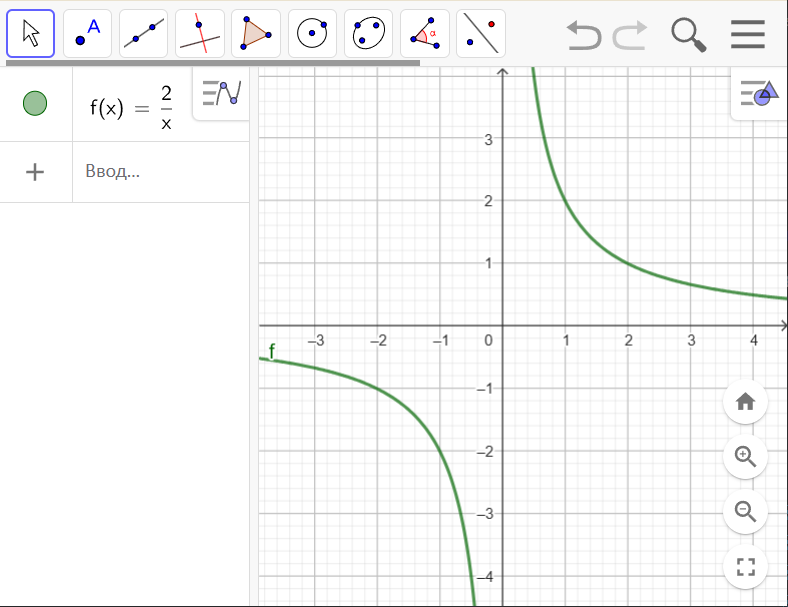 Якщо все зроблено правильно, то в полі для вводу ви побачите формулу \(f(x)=\frac{2}{x}\), а на координатній площині – графік функції \(f(x)=\frac{2}{x}\).
Якщо все зроблено правильно, то в полі для вводу ви побачите формулу \(f(x)=\frac{2}{x}\), а на координатній площині – графік функції \(f(x)=\frac{2}{x}\).
Покажемо, як можна побудувати в одній системі координат графіки декількох функцій.
Ще раз підкреслимо, що ми взяли інше ім'я для нової функції, а саме g. Якщо ви введете f(x) = 2, то раніше побудований графік функції f, а саме \(f(x)=\frac{2}{x}\), зміниться на \(f(x)=2\).
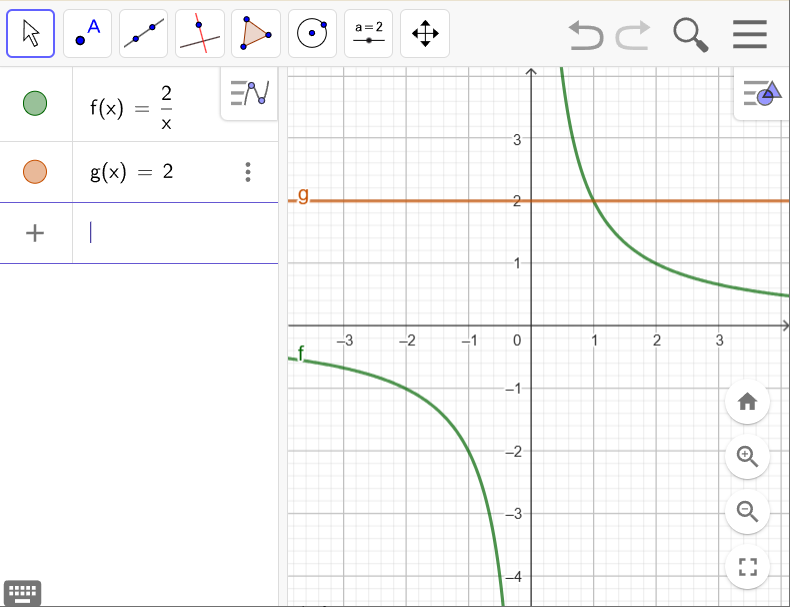 Якщо все зроблено правильно, то бачите на екрані два графіки функцій f і g. За бажанням також можна змінювати їхні кольори та стиль, щоб краще розрізняти їх.
Якщо все зроблено правильно, то бачите на екрані два графіки функцій f і g. За бажанням також можна змінювати їхні кольори та стиль, щоб краще розрізняти їх.
Про деякі правила введення формул, які задають функції в GeoGebra:
1. Коли ви вводите формулу в полі для вводу команд GeoGebra, то програма допомагає вам у цьому. Наприклад, ви натискаєте клавішу / – і весь подальший ввод буде в знаменнику утвореного дробу, поки ви не натиснете стрілочку \(\to\).
Так, якщо ви вводите вираз \(\frac{1}{2x}+1\) , то спочатку пишете 1/ . Тоді програма розуміє, що далі ви будете вводити знаменник дробу та показує це вам. Далі ви вводите 2x і хочете закінчити вводити знаменник, але поки ви не натиснете \(\to\), все, що ви друкуєте, належатиме до знаменника. Тобто правильно друкувати так: 1/2x\(\to\)+1.
Спробуйте ввести, наприклад, таку формулу: \(f(x) = \frac{1}{2}x+\frac{1}{3}\)
Підказка: f(x)=1/2\(\to\)x + 1/3 Enter
Або просто можете скопіювати в поле для вводу текст: f(x)=1/2 x + 1/3 . Цей прийом зручно використовувати тоді, коли ви вже маєте в текстовому вигляді готову формулу.
2. Десяткові дроби вводяться через крапку. Наприклад, дріб 0,27 вводимо так: 0.27
Наведемо ще декілька прикладів, як ввести формули, які задають функцію:
| Формула | Вводимо |
|---|---|
| \(f(x)=2x-3\) | f(x)=2x-3 |
| \(f(x)=-\frac{8}{x}+1\) | f(x)= -8/x\(\to\)+1 |
| \(f(x)= -\frac{8-x}{x}-0.2x+\frac{2}{3}\) | f(x) = -(8-x)/x\(\to\)-0.2x+2/3 |
Зазначимо, що в останньому прикладі обов'язково треба брати знаменник дробу в дужки. Якщо це не зробити, то отримаємо іншу формулу, а саме: \(f(x)= -8-\frac{x}{x}-0.2x+\frac{2}{3}\)
Потренуйтеся вводити формули в GeoGebra:
| \(f(x)=\frac{1}{5}-\frac{3}{x}\) |
| \(f(x)=\frac{2}{x}+x\) |
| \(f(x)=\frac{x-1}{x-2}\) |
Побудуйте в одній системі координат графіки функцій:
| \(f(x) = 2x + 3\); | \(g(x) = - \frac{6}{x}\) |
| \(f(x) = 1 - 3x\); | \(g(x) = 2 - \frac{3}{x}\) |
| \(f(x) = 3x - 4\); | \(g(x) = \frac{6 - x}{x}\) |
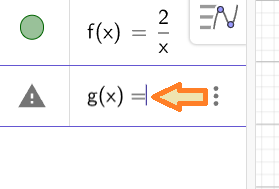 Для цього в поле вводу команд GeoGebra введемо
Для цього в поле вводу команд GeoGebra введемо